Pythagorus
Most of us have at some point learned the famous pythagorean equation, that for a right angled triangle, a²+b²=c² where c is the length of the hypotenuse.
E.g. if one side of the triangle is 5cm long, the side at right angles to it is 12cm, then the hypotenuse is 13cm.
There are many proofs of this, but I thought it would be good to record, what I think is the best.
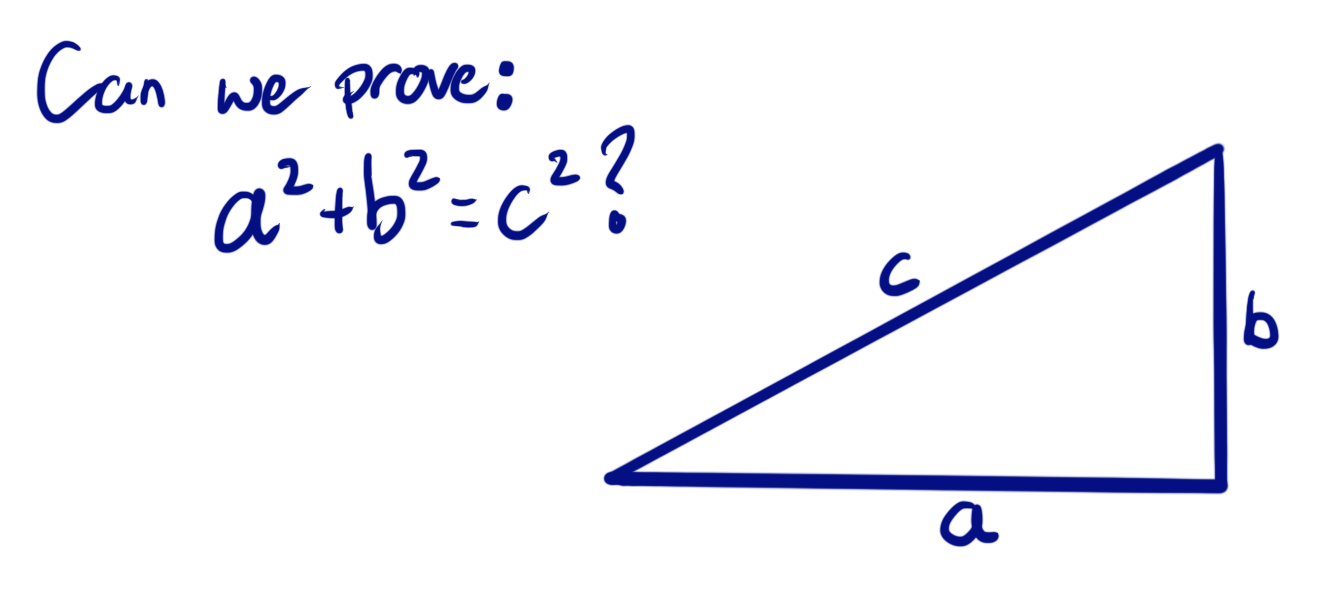
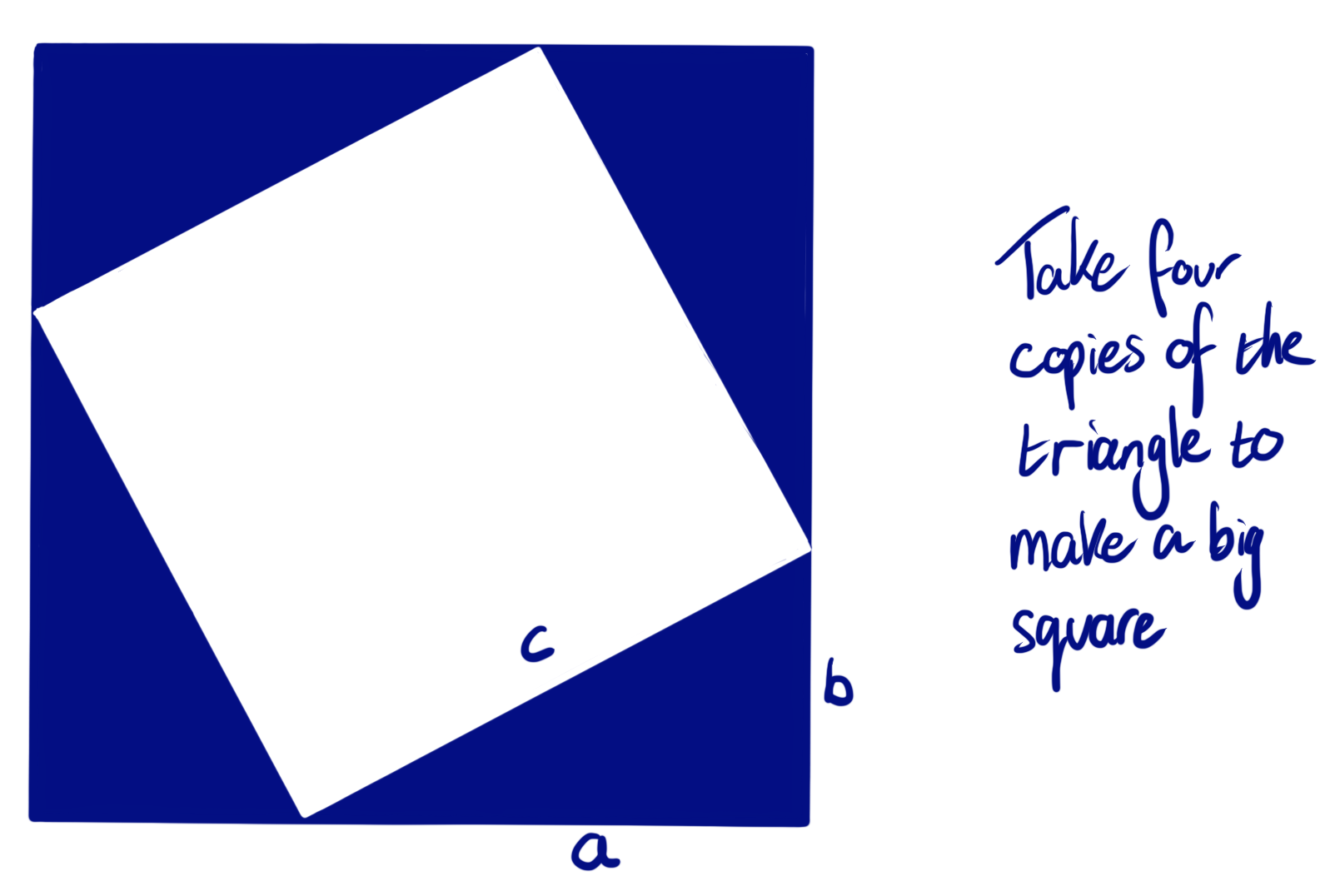
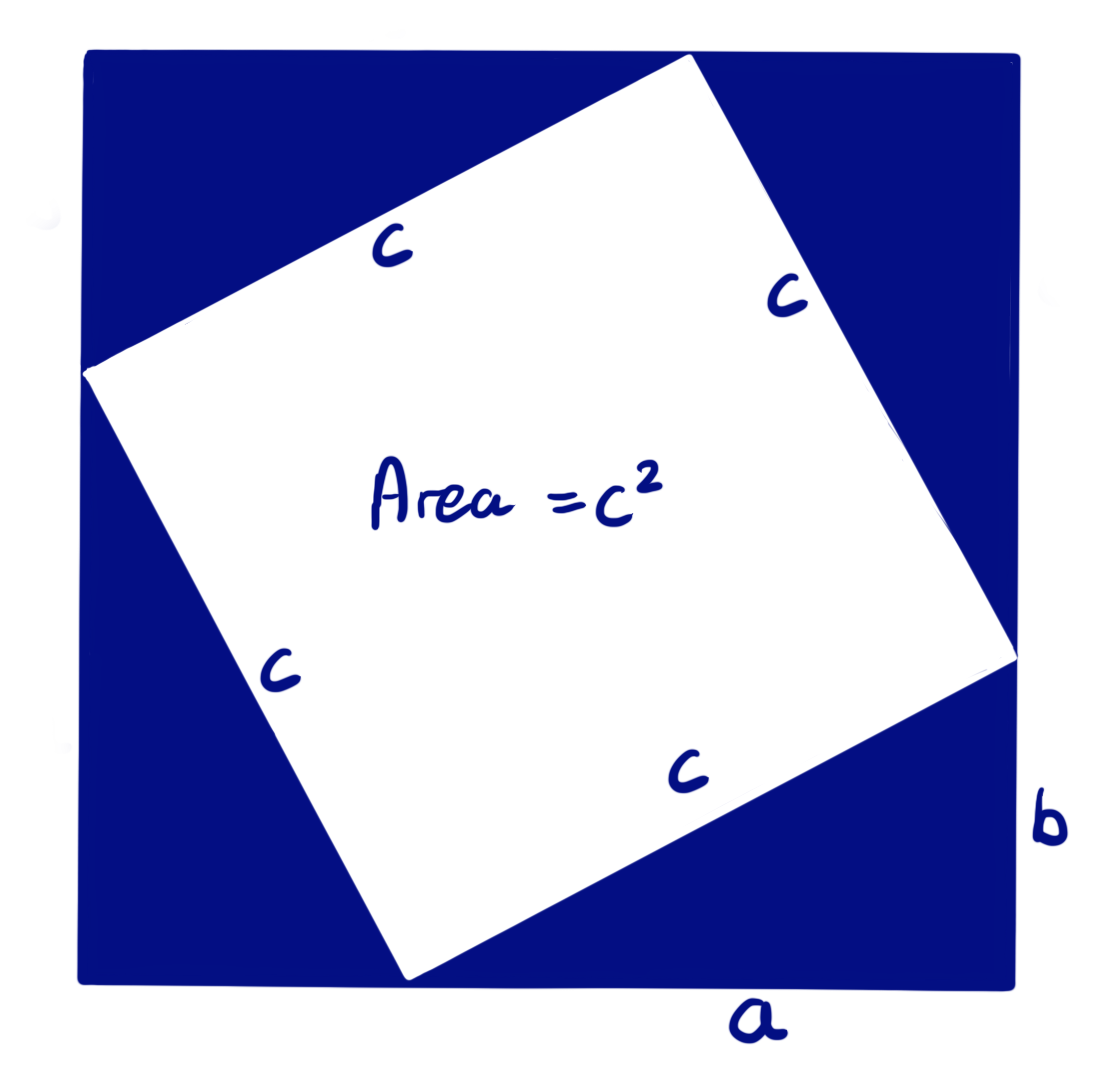
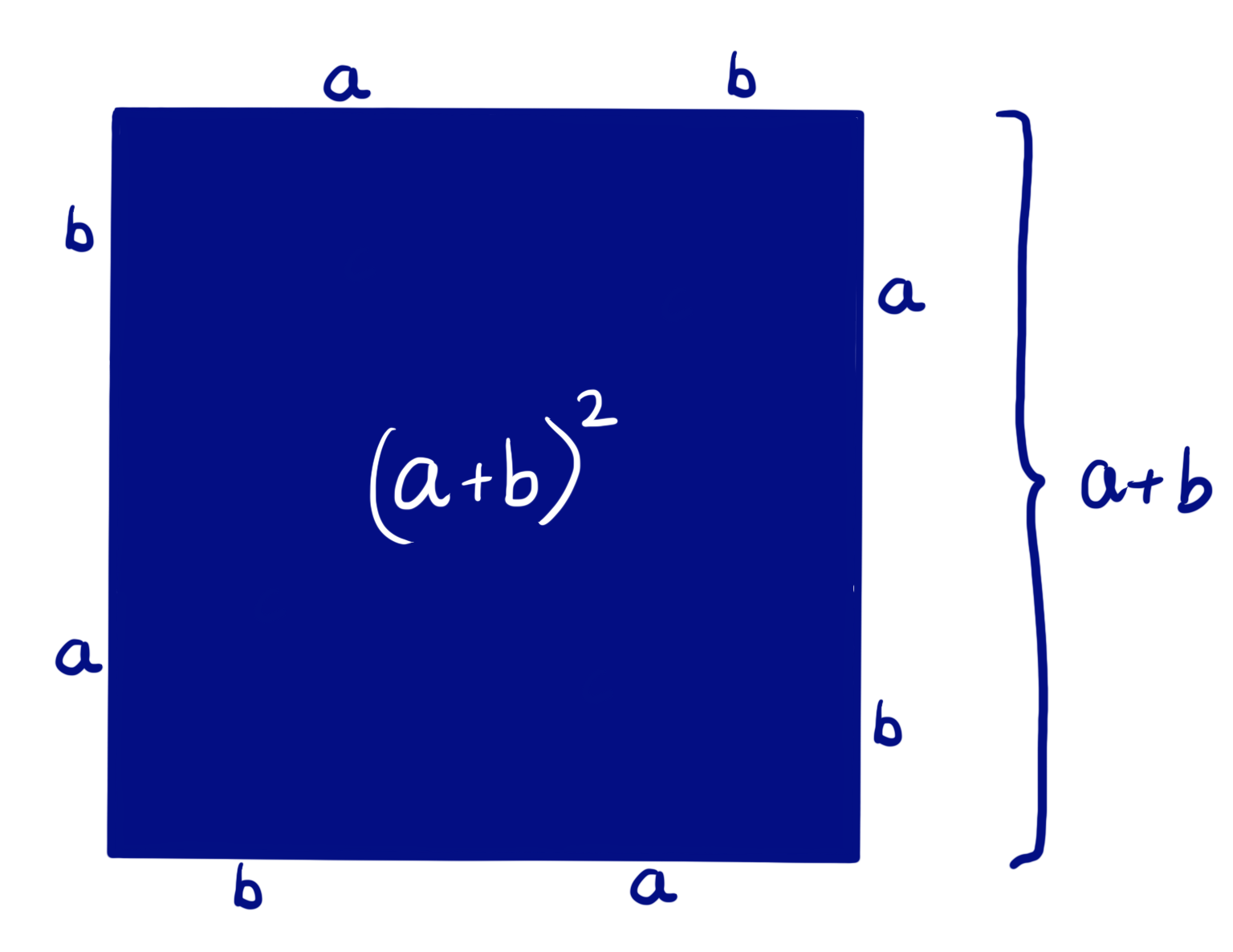
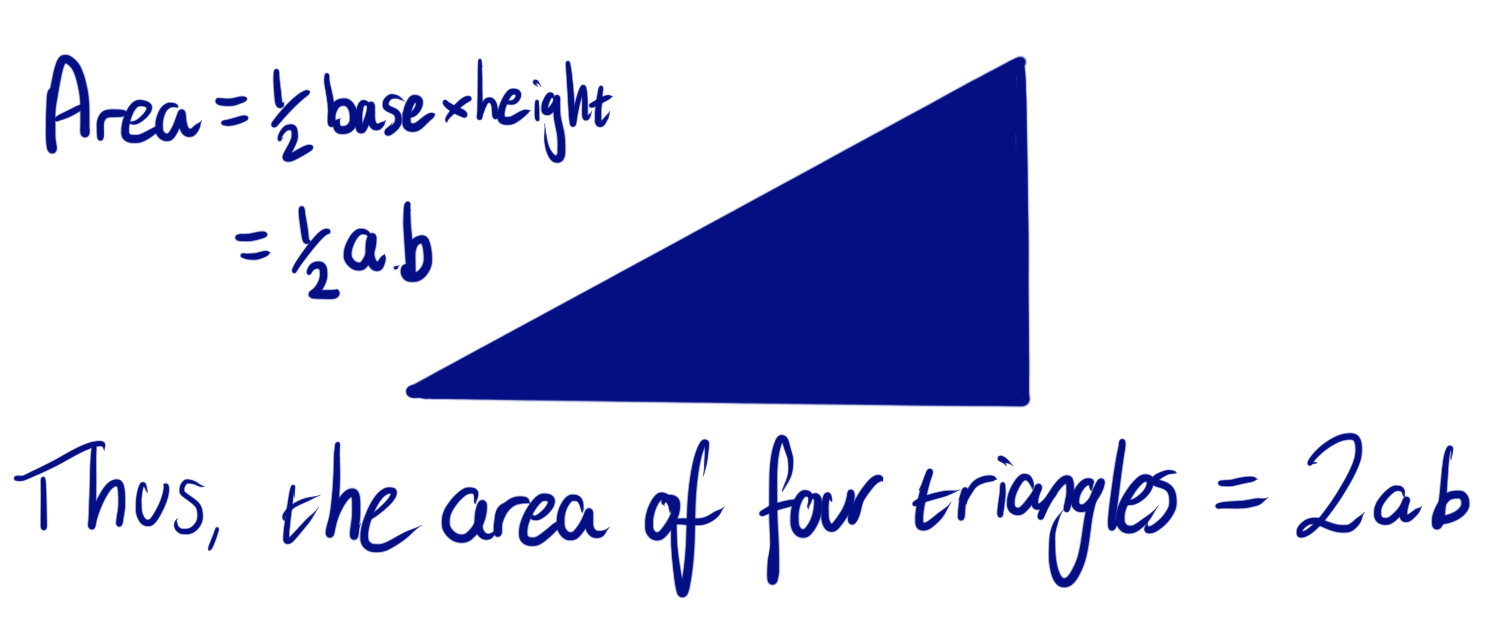
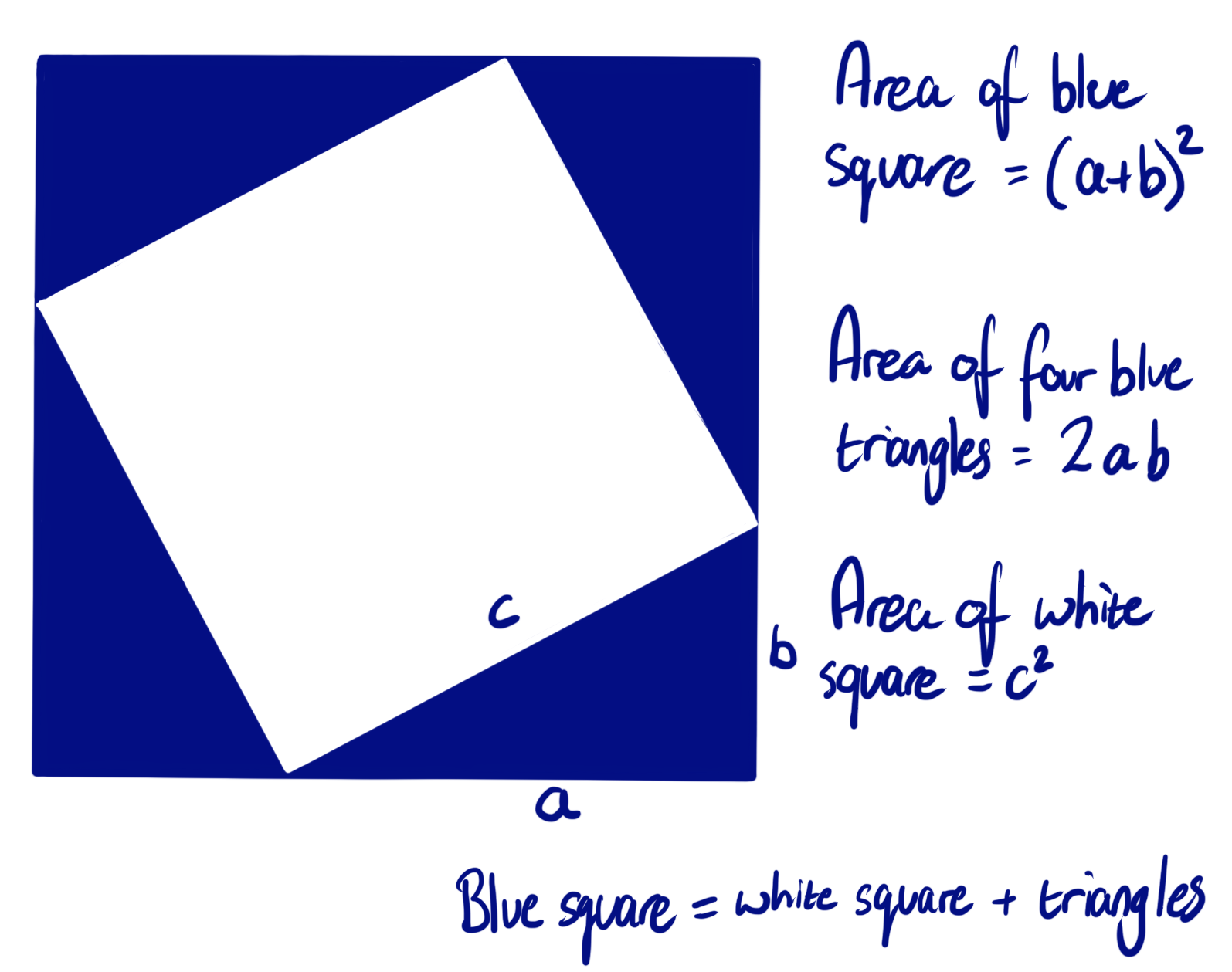
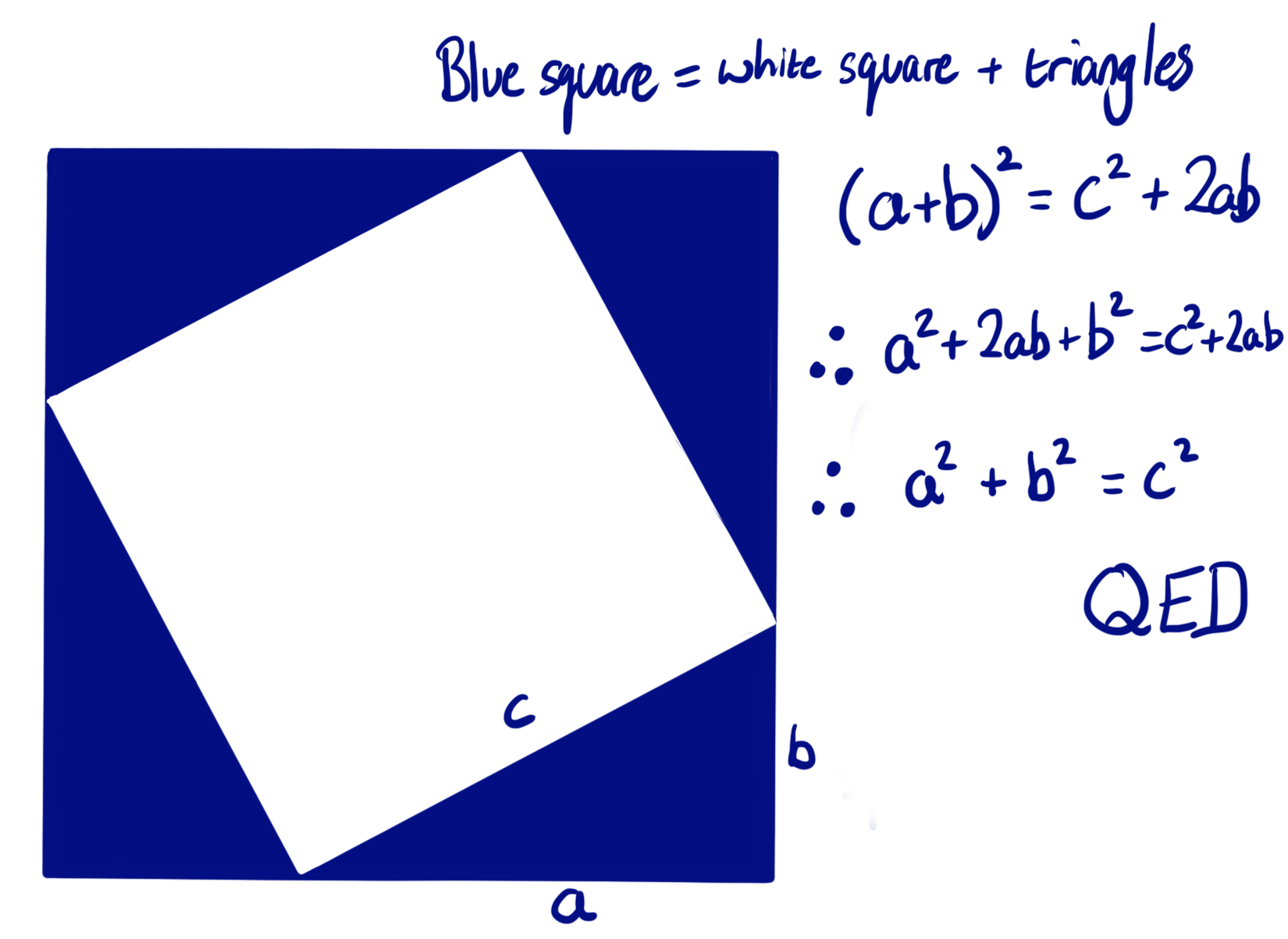
Photo Credit: Me
In short, examine the diagram below, made up of four triangles like the one shown here.
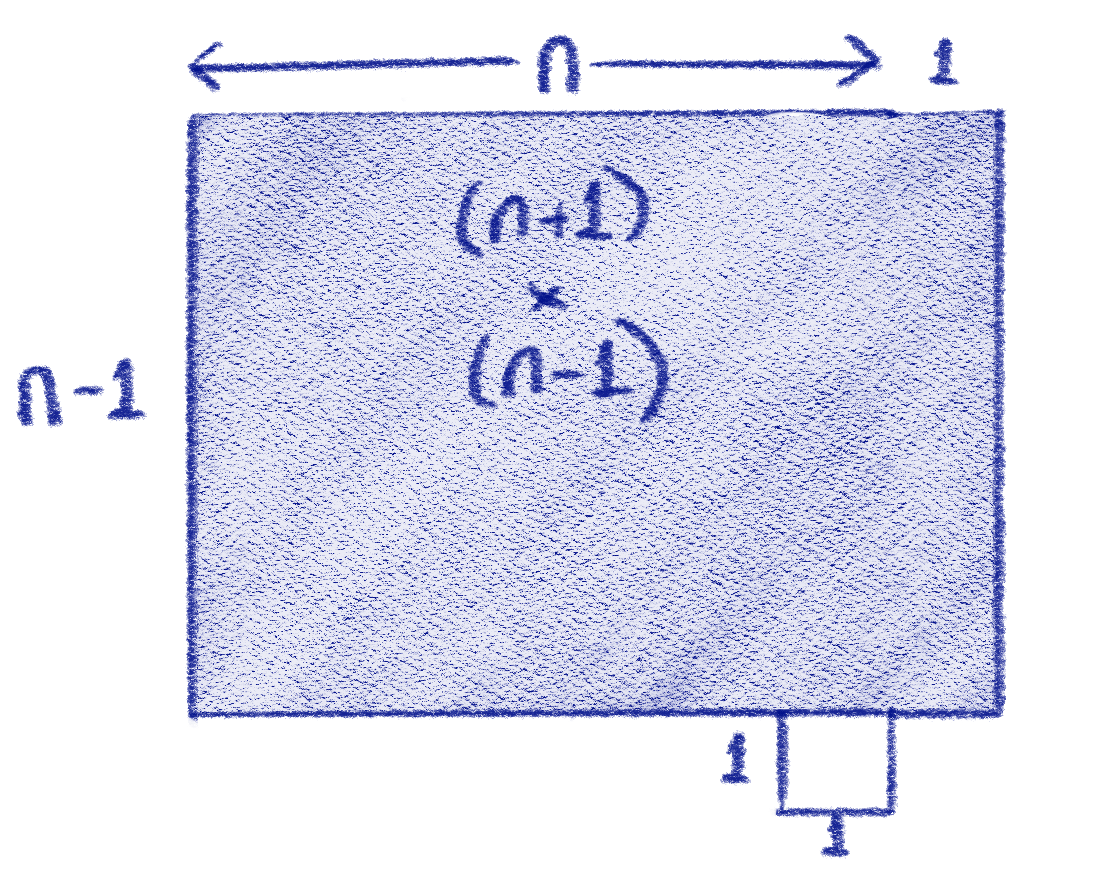
Blue square = white square + four triangles
(a+b)² = c² + 4×(½ab)
(a+b)² = c² + 2ab
a² + 2ab + b² = c² + 2ab
∴ a² + b² = c²
Pythagorus
An elegant proof
More Maths posts: